نقترح دراسة حركة قطرة مطر، كتلتها
1- ندرس حركة القطرة في حالة سقوط شاقولي في الهواء في جوّ هادئ (عدم وجود رياح). عبارة قوة الاحتكاك المؤثرة على القطرة هي:
- شعاع سرعة مركز عطالة القطرة،
- ثابت.
1.1- أعط عبارة دافعة أرخميدس
2.1- ندرس حركة سقوط القطرة على محور شاقولي
3.1- المحنى المرافق يعطي تغيرات سرعة سقوط القطرة بمرور الزمن:
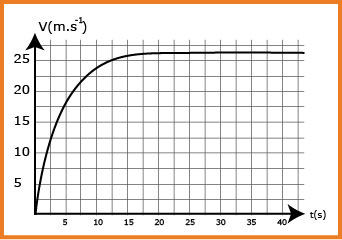
أ ) كيف يتغير تسارع القطرة بمرورالزمن؟ علّل.
ب) ما هي قيمة التسارع عند بلوغ النظام الدائم؟ قارن عندئذ قيم القوى المؤثرة على القطرة.
جـ) أوجد العبارة الحرفية للسرعة في النظام الدائم
د) حدّد، بيانياً، قيمة
2- نعتبر الآن أنّ قوة الاحتكاك ودافعة أرخميدس مهملتان أمام ثقل القطرة. عندما كانت القطرة تسقط شاقولياً، تعرضت فجأة إلى هبّة ريح مدّتها قصيرة جدّاً، أكسبتها سرعة أفقية
1.2- بتطبيق القانون الثاني لنيوتن، أوجد المعادلتين الزمنيتين لحركة القطرة
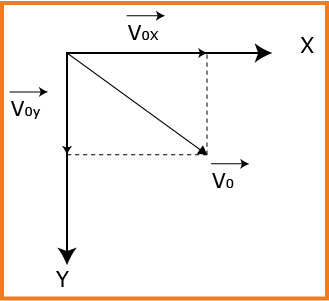
2.2- أوجد معادلة مسار القطرة، وحدّد طبيعته.
معطيات:
- تسارع الجاذبية الأرضية:
- الكتلة الحجمية للماء:
- الكتلة الحجمية للهواء:
1.1- عبارة دافعة أرخميدس:
ثقل القطرة أكبر
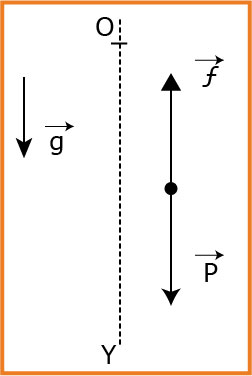
2.1- بتطبيق القانون الثاني لنيوتن على القطرة في المعلم الأرضي الذي نعتبره غاليلياً:
بالإسقاط على المحور
ومنه:
إذن
وهي من بالشكل:
حيث:
3.1- أ) تسارع القطرة
ب) عند بلوغ النظام الدائم يصبح
جـ) في النظام الدائم تصبح المعادلة التفاضلية:
ومنه:
د ) من البيان نجد
ومنه:
1.2- بتطبيق القانون الثاني لنيوتن:
بالاسقاط في المعلم المستوي
بالتكامل نجد:
وبالتكامل مرة أخرى نجد:
2.2- معادلة مسار القطرة: لدينا:
ومنه:
إذن: المسار عبارة عن قطع مكافئ.








